农历与公历的换算
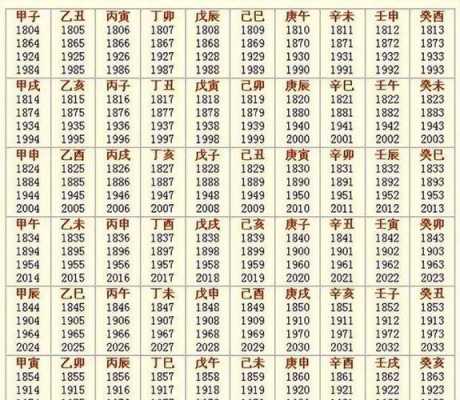
1、农历年的构成:农历年由天干地支两个序列组成。天干序列(A序列)包括:甲乙丙丁戊己庚辛壬癸10(0)。地支序列(B序列)包括:子丑寅卯辰巳午未申酉戌1亥12(0)。
2、由农历(干支年)推算公历年:公式:(天干序数 - 地支序数)÷ 2 × 10 + 3 + 天干序数 上述得数再加任意一个60的倍数即可得到对应的公历年份。例1:求丁丑年对应的公历年份。
3、- 首先,确定阴历年份对应公历的年份。使用公式:公历年份 = (阴历年份 - 1900)÷ 60 + 1900 + 1。例如,阴历的2019年对应的公历年份计算为20184,即2019年。- 其次,计算阴历正月初一对应的公历日期。
4、阳历和阴历之间是不能换算的,二者采用的计算方法不同,没有特殊关系可以查询,只能分别计算。公历是阳历的一种,阳历就是以地球绕太阳公转的运动周期为基础而制定的历法。
农历和公历怎么换算
1、农历年公历农历转换的构成公历农历转换:农历年由天干地支两个序列组成。天干序列(A序列)包括:甲乙丙丁戊己庚辛壬癸10(0)。地支序列(B序列)包括:子丑寅卯辰巳午未申酉戌1亥12(0)。
2、由农历(干支年)推算公历年:公式:(天干序数 - 地支序数)÷ 2 × 10 + 3 + 天干序数 上述得数再加任意一个60公历农历转换的倍数即可得到对应公历农历转换的公历年份。例1:求丁丑年对应的公历年份。
3、农历与公历的换算基于两个基本周期:回归年和朔望月。回归年代表太阳从春分点回到春分点的时间,约为362422日,而朔望月则是月球绕地球一周,从新月到下一次新月或满月所需的时间,大约是25306日。由于这两个周期的差异,每19年会多出大约7个额外的日子,这就需要插入闰月来调整。
4、查历书:最直接的换算方式是通过历书或网络工具查询。历书中会详细列出某年农历对应的公历日期。 计算方式:虽然具体的计算方式较为复杂,但大致上可以通过一些算法和公式进行换算。这需要公历农历转换了解农历和公历的基本规律,并结合具体的年份和月份进行推算。
公历跟农历怎么算
1、由农历(干支年)推算公历年:公式:(天干序数 - 地支序数)÷ 2 × 10 + 3 + 天干序数 上述得数再加任意一个60公历农历转换的倍数即可得到对应的公历年份。例1:求丁丑年对应的公历年份。
2、公历和农历是两种不同的历法系统公历农历转换,它们在计算上没有直接的换算关系公历农历转换,因此不能直接相互转换。阳历,即公历,是以地球绕太阳运行周期为依据,即回归年,共365天5小时48分46秒,平年只计365天,不考虑尾数,每四年会出现一个闰年,闰年2月有29天。
3、要将公历日期转换为农历日期,可以采用特定的数学公式。设:公元年数减去1977(或1901)等于4Q加上R。则:阴历日期等于14Q加上6倍的(R+1)加上当年日期序数减去25n。其中,Q、R、n都是自然数,且R小于4。
4、首先,两者出处不同,公历等于阳历,是世界通用的日期,也是我们平常的日期。农历等于阴历,是我国古代用来农耕的日期,也就是日历下面的小字所表示的日期。其次,两者算法不同,阳历是以地球绕太阳一周为一年所定出的历法,农历是以月亮绕地球为一个月,12个月为一年(闰年为13个月)所定出来的历法。
5、阴历阳历换算方法有公式法、月干口诀法等。公式法 月干公式为:月干=年干数×2+月份。例:1997年8月,月干=4(1997年天干数)×2+7(农历月份)=15大于10则除以10余5,查代数知为戊。阳历和阴历之间是不能换算的。
农历和阳历的换算
1、阳历和阴历之间是不能换算公历农历转换的公历农历转换,二者采用公历农历转换的计算方法不同公历农历转换,没有特殊关系可以查询,只能分别计算。公历是阳历的一种,阳历就是以地球绕太阳公转的运动周期为基础而制定的历法。
2、阴历和阳历的换算方法包括公式法、干支纪年法等。以公式法为例,假设某年的天干数为X,月份为Y,则月干的计算公式为:月干 = X × 2 + Y。例如,1997年8月的月干计算如下:月干 = 4 × 2 + 7 = 15。由于15大于10,需要除以10,余数为5,对应的天干为戊。
3、阳历和阴历之间是不能换算的。阴历,中国传统历法之一,也被称为旧历、汉历、古历等,辛亥革命后改用西方太阳历(公历),而近现代使用的农历属于阴阳合历,也就是阴历和阳历的合历。
4、阴历和阳历的换算方法:阴历和阳历是两种不同的历法,阴历以月亮的月相周期来设置月份,而阳历则以地球绕太阳转动的周期为基准来计算时间。二者之间的转换可以通过特定的历法规则进行。但由于涉及的历法知识比较复杂,通常采用一些专业的转换工具或者历书来得到准确的换算结果。以下简单介绍换算过程及注意事项。
5、公历和农历之间没有直接的公式转换,因为两者不是简单的数学关系。公历是基于地球围绕太阳公转的周期,而农历是基于月亮的圆缺周期。两者之间的转换涉及到多变的月亮相位和地球公转位置,因此不能简单地通过一个公式来实现。





